27、WebGL三维旋转的原理及矩阵的推导

# 1、旋转

旋转笔平移要复杂一些。为了描述旋转，你必须要指明以下三个条件。

旋转轴
旋转方向，顺时针或者逆时针
旋转角度

旋转中，右手握拳，大拇指伸直并指向其旋转轴的正方向，那么右手其余几个手指久指明了旋转的方向，因此沿着逆时针旋转的正旋转又可以称为右手法则旋转。它是WebGL程序的默认设定。下面我们通过计算一个绕Z轴旋转的模型，来推导选轴公式和旋转矩阵。

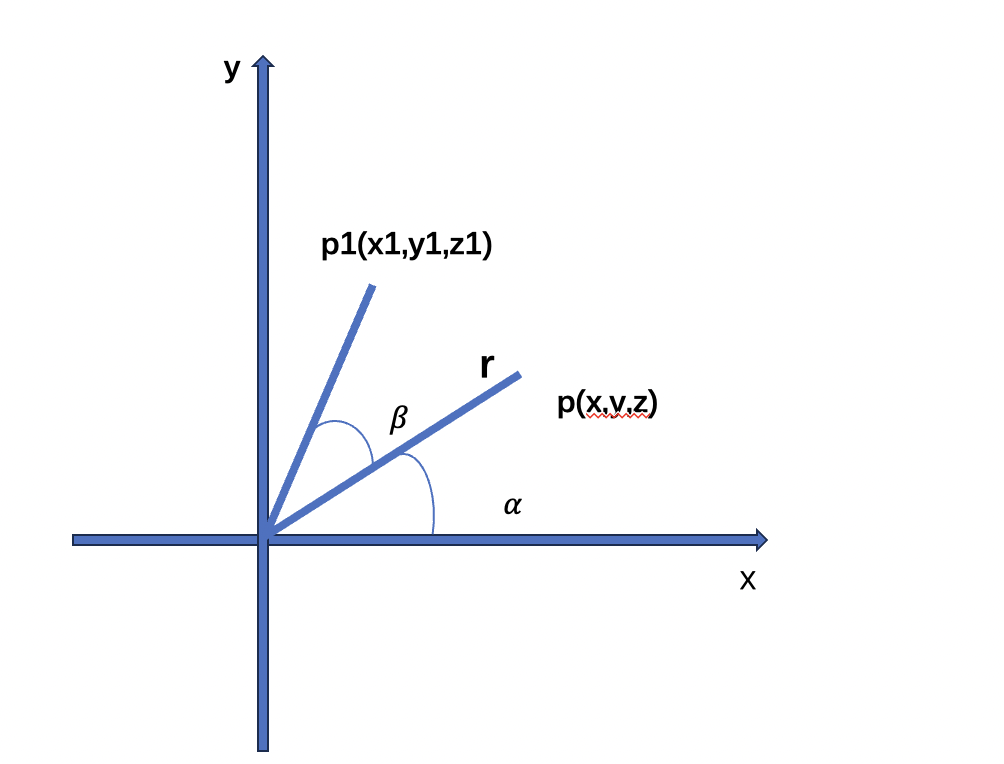
上图中，r 是从原点到 p点的距离。而𝛼则是 X轴旋轴到p点的角度，用着两个变量可以得出 p 点的坐标。

x = r*cos(𝛼)

y = r*san(𝛼)

1
2
3

同样我么，也可以用 𝛼``𝛽 和r来表示点 p1的坐标。

x1 = r*cos(𝛼+𝛽)
y1 = r*sin(𝛼+𝛽)

1
2

利用我们学过的三角函数两角和公式。

sin(𝛼±𝛽) = sin(𝛼)cos(𝛽) ± cos(𝛼)sin(𝛽)
cos(𝛼±𝛽) = cos(𝛼)cos(𝛽) ∓ sin(𝛼)sin(𝛽)

1
2

根据三角和公式

x1 = r*cos(𝛼+𝛽) = r(cos(𝛼)cos(𝛽) - sin(𝛼)sin(𝛽))
y1 = r*sin(𝛼+𝛽) = r(sin(𝛼)cos(𝛽) + cos(𝛼)sin(𝛽))

1
2

最后将 r= x/cos(𝛼)和 r = y/san(𝛼) 带入上面的公式可以得到。

x1 = x * cos(𝛽) - y * sin(𝛽)
y1 = x * sin(𝛽) + y * cos(𝛽)
z1 = z

1
2
3

然后我们可以根据旋转的角度𝛽将 sin(𝛽)和 sin(𝛽)的值传递给顶点着色器，然后得到旋转后的顶点坐标，就可以实现旋转的效果了。顶点着色器中的代码如下所示：

attribute vec4 a_Position;
uniform float u_cosB,u_sinB;
void main(){
    gl_Position.x = a_Position.x * u_cosB - a_Position.y * u_sinB;
    gl_Position.y = a_Position.x * u_sinB - a_Position.y * u_cosB;
    gl_Position.z = a_Position.z;
    gl_Position.w = 1.0;
}

1
2
3
4
5
6
7
8
9

在js中的代码如下所示

const ANGLE = 90.0; 
const radian = Math.PI * ANGLE / 180.0; // Convert to radians
const cosB = Math.cos(radian);
const sinB = Math.sin(radian);

const u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');
const u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');
gl.uniform1f(u_CosB, cosB);
gl.uniform1f(u_SinB, sinB);

1
2
3
4
5
6
7
8
9

具体的demo 可以参考旋转 (opens new window) 。

# 2.旋转矩阵的推导

可以使用以下的矩阵能来实现三角形的旋转。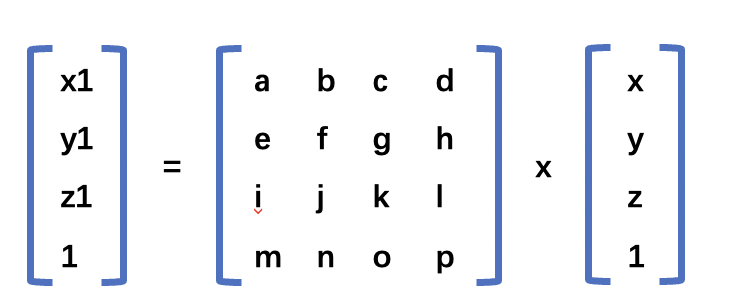上面矩阵的乘法结果如下所示。

x1 = ax + by + cz + d = x * cos(𝛽) - y * sin(𝛽)
y1 = ex + fy + gz + h = x * sin(𝛽) + y * cos(𝛽)
z1 = ix + jy + kz + l = z
1  = mx + ny + oz + p

1
2
3
4

根据上面的乘法结果可以得出平移矩阵的结果。

a = cos(𝛽),b = -sin(𝛽),c = 0,d =0; 
e = sin(𝛽),f = cos(𝛽), g = 0,h = 0;
i = 0,j = 0,K = 1,l = 0;
m = 0,n = 0,o = 0,p = 1;

1
2
3
4

所以可以得到平移矩阵如下所示

具体的demo 可以参考旋转-矩阵 (opens new window) 。

阅读量：

# 1、旋转

# 2.旋转矩阵的推导

评 论：

评论：